浅谈非球面二次曲线常数

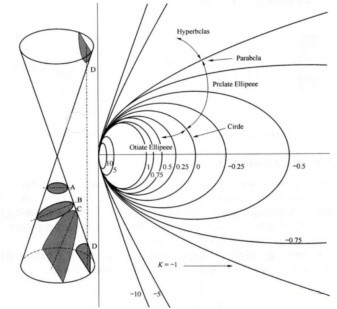
一个光学面是不是非球面，首先看这个面型参数有没有二次曲线常数（conic constant）。那么这个二次曲线常数是怎么来的呢？

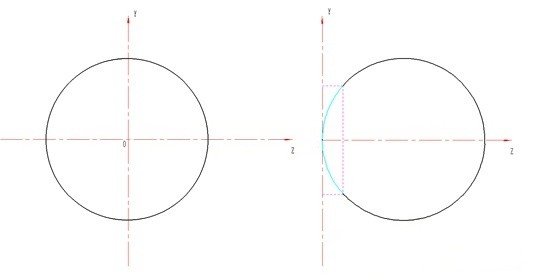
上面下图中，圆形的圆心刚好位于坐标系统的原点，此时这个圆的方程为：

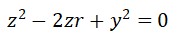
如果将圆在图形坐标系统中移动，让圆和纵坐标相切，那么平移之后的圆方程为：

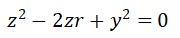
介于今天我们讨论的是光学面型，所以我们重点关注一下平移后圆形曲线框里青色的区域。我们假设青色曲线不是球面，而是一个非球面，那么这个非球面的方程为：

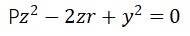
其中P=1+K，K=-e²，e为离心率【e²=（a²+b²）/a²，a是二次曲线的半长轴，b是二次曲线的半短轴】，这里的K就是ZEMAX软件里的二次曲线常数。

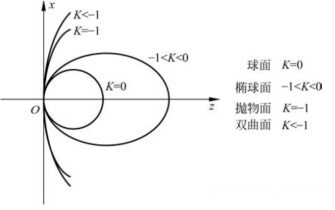
从以上图可以看出，当K=0时，曲线是球面，随着K值偏离0,且绝对值越大，截面的曲线就越平缓，试想一下，当K值的绝对值趋近于无穷大时，就无限接近于平面。因此我们可以想象，对于加工而言，K值的变化很大程度上会影响其面型的工艺性，K值绝对值越接近0越好加工。且根据经验，一般来说这个绝对值要小于等于10。

本文内容转载自，公众号“佳文光学”《浅谈非球面二次曲线常数》，版权归原作者所有，仅用于学习、交流用途。如涉及版权问题或侵权内容，请及时联系我们（手机|微信：13697356016），我们将第一时间处理或删除。